【漫画でIT入門】とあるIT企業の社員活動日誌 第28話「プログラミング学習のすゝめ⑭ データ構造について」
パソコンを使う人のありそうでなさそうなお話や、ガジェットのお話を漫画で紹介させていただくコーナーです。
とあるIT企業に務める彼女たちは日々楽しく真面目に業務に励んでいます。その中で、起こったハプニングや困った事などを活動日誌を通して覗き見していきましょう。
※当ブログは、アフィリエイトプログラムに参加して商品を紹介しております。当ページのリンクを介して商品を購入すると著者に収益が発生することがあります。
【漫画で入門】「とあるIT企業の社員活動日誌」各話一覧はこちら

目次
データ構造について
前回は、プログラミングとデータ構造・アルゴリズムについて簡単にお話しました。
今回はデータ構造に注目してお話をしたいと思います。
プログラミング言語「Pascal」の開発者であるN.Wirthは「アルゴリズム+データ構造=プログラム」という言葉を残しています。アルゴリズムは処理の手順、データ構造はデータの配置・管理する方法のことで、この2つがプログラムを構成していることを端的に表現しています。
代表的なデータ構造
データ構造①「リスト構造」
リスト構造は要素をチェーンのように繋ぐデータ構造です。
要素はデータを格納するデータ部と次に繋がる要素(次要素)の位置情報を持つポインタ部から構成されています。
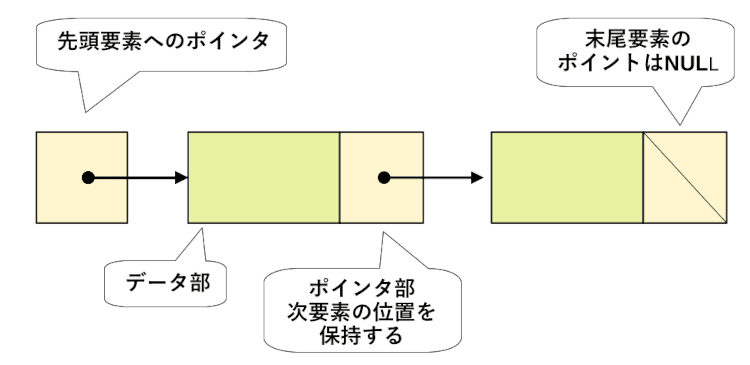
要素の位置は一つ前の要素が保持していますが、これ音は別にリストの開始位置(先頭要素)を指すポインタを別途用意しなければなりません。
ポインタの内容は、次要素が格納されたメモリのアドレスなどです。最終要素のポインタはNULL(空値)です。
図のような一方向のリストは単方向リストと呼ばれます。このリストは先頭要素からポインタを辿りながらデータを順次参照します。
・要素の追加、削除
リスト構造への要素の追加・削除右派、それを行う前後のポインタを修正するだけで簡単に実現することが出来ます。
これは挿入場所を確保しなければならない”配列”と比べると非常に優れた性質です。
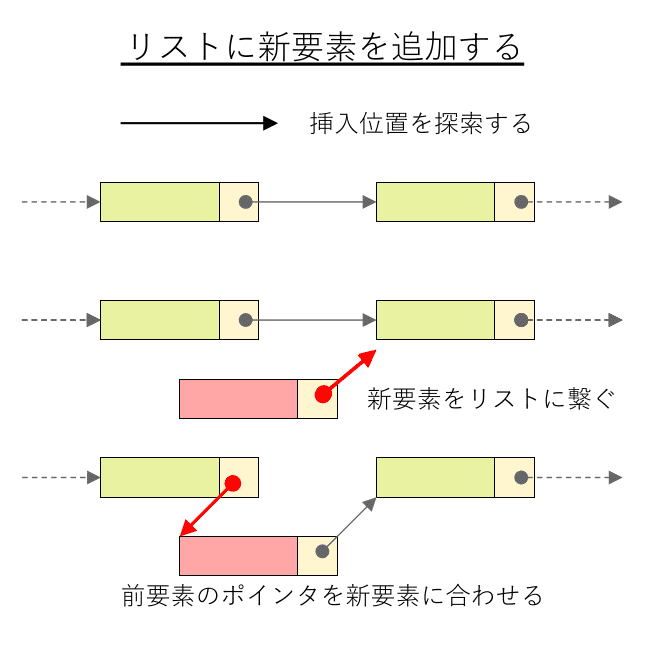
リストへの挿入は
1. 挿入位置の検索
2. 新要素のポインタを挿入位置の新要素に合わせる
3. 挿入位置の前要素のポインタを新要素に合わせる
という手順で行います。
データの削除は
1. 削除要素の検索
2. 削除要素の前要素を、削除要素の次要素へつなぐ
という手順になります。
リスト構造に対する処理は計算量(データ数nに対してどれだけの処理が必要かを表すもの。処理の繰返し((ループ))回数で評価する。)で評価出来ます。
挿入・削除位置の探索はO(n)の処理ですが、それ以外はO(1)です。先頭への追加・削除であれば、検索事態が不要になるためO(1)の計算量で処理が可能です。
逆に末尾に対する追加・削除は最も時間を要します。
・リストの改良
ポインタのもたせ方によって、さまざまなリストを構築することが出来ます。

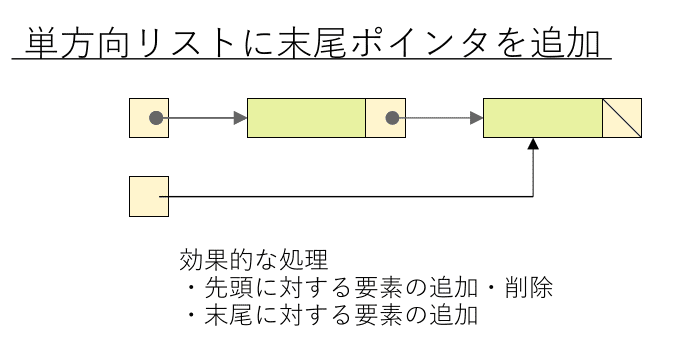

単方向リストに末尾ポインタを設けると、末尾要素をO(1)で参照出来るため、末尾への追加効率が高くなります。
ただし、末尾要素の削除効率は改善されません。
なぜなら削除には「末尾の一つ前の要素」を参照する必要がありますが、リストは逆方向には辿れないため、先頭に戻ってやり直さなければならないからです。
双方向リストにすれば、末尾から先頭方向にもリストを辿る事が出来ます。
末尾ポインタを徹前に戻すことは容易なため、末尾要素の削除効率も改善されます。
データ構造②「スタック」
スタックは「後入れ先出し(LIFO:Last In First Out)」の性質を持つデータ構造です。
一方だけ空いた管にデータを格納するようなイメージを持つと分かり易いです。

スタックへデータを格納する操作をPUSH、取り出す操作をPOPと呼びます。
スタックは「一方だけ空いた」管なので、PUSH/POPは同じ口から行われます。
結果として後に格納したデータほど先に取り出されます。
図はA、B、Cの順にデータをPUSHした状態を表します。最初のPOPでデータC、次のPOPでデータB、最後のPOPでデータAが取り出されます。
・スタックの利用法
スタックは様々な場面で利用されます。
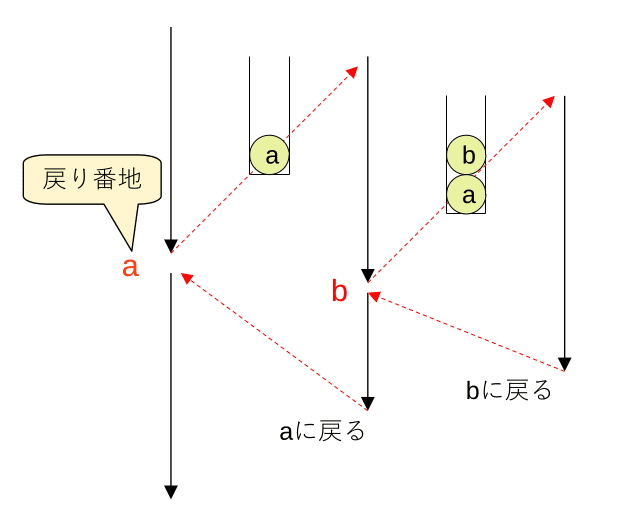
①プログラム呼び出し時の戻り番地の管理
関数やサブルーチンが処理を終えた時に、それを呼び出した場所に正しく戻る必要があります。
その為、戻る番地をスタックに格納してから関数やサブルーチンを呼び出すようにします。(より正確には戻り先アドレスや待機するレジスタの内容が格納される)
関数やサブルーチンが処理を終えると、スタックから戻り番地をPOPして呼び出し元に戻ります。
②逆ポーランド記法の演算
逆ポーランド記法で記述された演算式は、一つのスタックだけで計算できるのが特徴です。
具体的には演算式を左から順に見ながら、次の手順を繰り返します。
最終的には、計算式の解がスタックに格納された状態で終了します。
• 数値であればスタックに格納する
• 演算子であればスタックから数値を2つPOPして計算し、計算結果をスタックに格納する
データ構造③「キュー」
キューは「先入れ先出し(FIFO:First In First Out)」の性質を持つデータ構造です。
両端(入り口と出口)が空いた管にデータを格納するイメージを持つと分かり易いです。
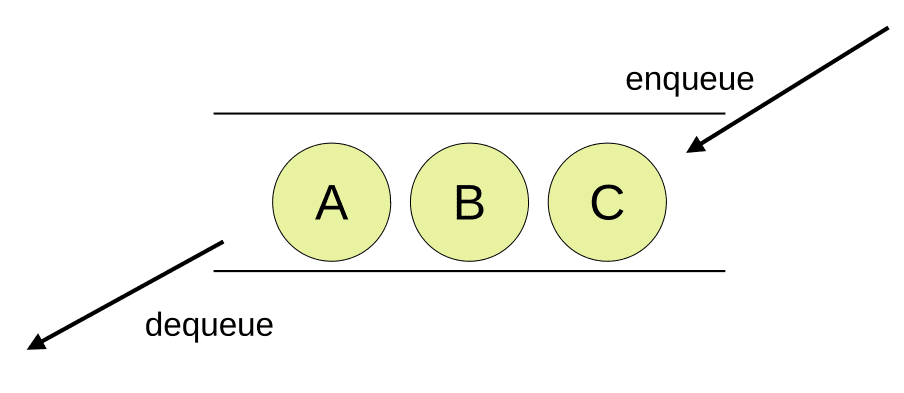
キューへデータを格納する操作をエンキュー(enqueue)、取り出す操作をデキュー(dequeue)と呼びます。
入り口と出口が異なるので、格納した順にデータを取り出せます。
キューは行列など、順番をもつ要素の管理に向いてます。
生成したタスクの管理や、到着したジョブの管理などはキューの代表的な利用法です。
データ構造④「木構造」
木構造は親子関係で階層構造を表すデータ構造です。
親は複数の子を持つことが出来ますが、子は一つの親しか持てません。
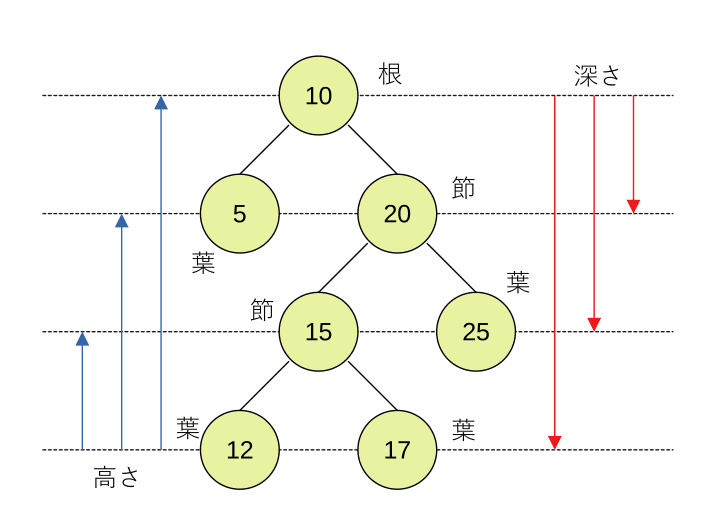
木の構成要素を節(node)と呼びます。特に最上位の節を根(root)、子をもたない節を葉(leaf)と呼ぶことがあります。
根から数えた階層数を深さ、最下位層の葉から数えた階層数を高さと呼びます。根の高さは木全体の高さになります。
・二分木
各節が最大二つの子を持てる木を、二分木と呼びます。上記図は高さ3の二分木の例です。
高さがnの二分木は最大2n+1-1個の節をもつことが出来ます。節の数がnである二分木の高さは、およそlog2nとなります。
・2分探索木
2分探索木(binary search tree)とは、次の2つの条件がすべての節に成り立つ二分木で、探索に向いたデータ構造です。
• ある節の左部分木(左の子に繋がる部分木)に属する節の値は、その節の値より小さい
• ある節の右部分木に属する節の値は、その節の値より大きい
上記図は2分探索木の条件を満たしています。
2分探索木は根から枝を降りるように探索を進めます。具体的には、探索節が節の値より小さければ左に折り、そうでなければ右に降ります。これを探索が成功するか、降りれる枝がなくなるまで繰り返します。(2分探索木の節の数がnの時、探索の計算量はO(log2n)となる)
・ヒープ
根から深さの浅い順に、節を左詰めにした気を完全二分木と呼びます。
完全二分木の中で、どの親子についても一定の大小関係が成立する木がヒープ(heap)です。
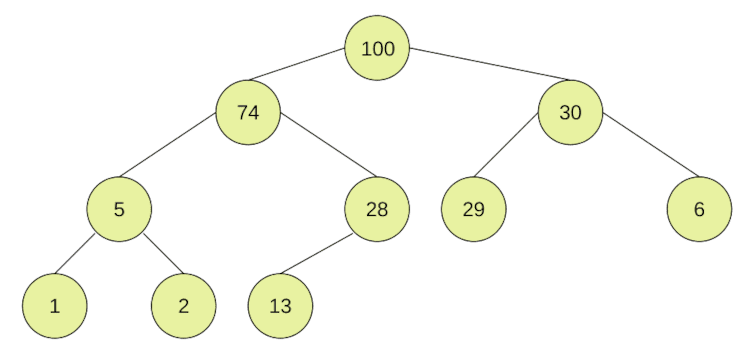
上記図は「親≧子」が成立するヒープの例です。
「親≧子」が成立するとき、根の値は最大値になります。
逆に「親≦子」が成立するとき、根の最小値になります。
ヒープは最大値や最小値を効率よく取り出す事ができるデータ構造です。
・木の巡回
木に含まれるすべてのデータを処理することもあります。
このような処理では、木のすべての節をもれなく巡回する必要があります。
この方法には大きく深さ優先順と幅優先順があります。
• 深さ優先順・・・子があれば子を優先して巡回する
• 幅優先順・・・兄弟を優先して巡回する
木の巡回においては「どのタイミングで節を処理するか」によって、節の訪問順序は大きく変わります。
データ構造を理解するメリット
データ構造を学ぶことには多くのメリットがあります。以下にその一部を挙げます。
①効率的なプログラムの作成
データ構造は、データを効率的に格納し、検索や挿入などの操作を高速に行うための方法を提供します。
適切なデータ構造を選択し、適切に使用することで、プログラムの実行速度を向上させることができます。
②複雑な問題の解決
データ構造は、複雑なデータや問題を効率的に処理するためのツールを提供します。
例えば、グラフや木のデータ構造を使用することで、ネットワークや階層的な関係を持つデータを効率的に解析することができます。
③メモリ管理の最適化
データ構造は、メモリの使用を最適化するための方法を提供します。
例えば、配列は連続したメモリ領域を使用するため、メモリのアクセスが高速です。
一方で、リストやツリーなどの動的なデータ構造は、必要な分だけメモリを確保するため、メモリの使用を効率化します。
④問題解決能力の向上
データ構造を学ぶことで、問題解決能力が向上します。
異なるデータ構造を理解し、適切に選択する能力は、プログラミングやコンピュータ科学の分野での問題解決能力を高めます。
⑤コードの再利用性と保守性の向上
データ構造を適切に使うことで、コードの再利用性と保守性が向上します。
データ構造を抽象化し、適切に設計することで、異なるプログラムやシステムで同じデータ構造を再利用することができます。
⑥アルゴリズムの理解
データ構造はアルゴリズムと密接に関連しています。
データ構造を理解することで、アルゴリズムの動作や性能を深く理解することができます。
さらに学べるおすすめ書籍
・世界標準MIT教科書 アルゴリズムイントロダクション 第4版 第1巻 基礎・ソートと順序統計量・データ構造・数学的基礎
漫画作者紹介

あとがきイラスト


